ভৌত রাশি ও পরিমাপ: বিজ্ঞানের ভিত্তিপ্রস্তর

ভূমিকা

পদার্থবিজ্ঞান হচ্ছে প্রকৃতির নিয়ম-নীতি বোঝার একটি পদ্ধতিগত প্রচেষ্টা, যেখানে আমরা বিভিন্ন ভৌত রাশি পরিমাপ করে তার কার্যকারণ ব্যাখ্যা করার চেষ্টা করি। বিজ্ঞানচর্চার প্রাথমিক ধাপই হলো পর্যবেক্ষণ ও পরিমাপ। দৈনন্দিন জীবনে আমরা প্রতিনিয়ত নানা ঘটনা ও পরিবর্তন প্রত্যক্ষ করি—গাড়ির গতি, পানি ফোটার সময়, বা একটা বল মাটিতে পড়ে যাওয়া। এসব ঘটনাকে বিশ্লেষণ করতে হলে সুনির্দিষ্টভাবে পরিমাপ করা জরুরি। আর এই পরিমাপের পেছনে নির্ভর করে রয়েছে ভৌত রাশির ধারণা।

পদার্থবিজ্ঞানের পরিসর

পদার্থবিজ্ঞান প্রকৃতির মৌলিক নিয়ম এবং নীতিগুলির অধ্যয়ন। এটি মহাবিশ্বের ক্ষুদ্রতম কণা থেকে শুরু করে অতিকায় গ্যালাক্সি পর্যন্ত সমস্ত কিছুর আচরণ এবং মিথস্ক্রিয়া ব্যাখ্যা করার চেষ্টা করে। ফলস্বরূপ, পদার্থবিজ্ঞানের পরিসর অত্যন্ত বিস্তৃত এবং এটিকে বিভিন্ন শাখায় বিভক্ত করা যেতে পারে। নীচে কিছু প্রধান শাখা এবং তাদের আলোচনার ক্ষেত্রগুলি উল্লেখ করা হলো:

প্রধান শাখা

• বলবিদ্যা (Mechanics)

  বস্তুর গতি এবং স্থিতিশীলতা, বলের প্রভাব এবং শক্তির ধারণা নিয়ে আলোচনা করে। এর মধ্যে নিউটনের গতিসূত্র, মহাকর্ষ, ঘর্ষণ ইত্যাদি অন্তর্ভুক্ত।

• তাপগতিবিদ্যা (Thermodynamics)

  তাপ, তাপমাত্রা, এবং শক্তির অন্যান্য রূপের মধ্যে সম্পর্ক নিয়ে আলোচনা করে। এটি ইঞ্জিন, রেফ্রিজারেটর এবং অন্যান্য তাপ-সম্পর্কিত প্রযুক্তির ভিত্তি স্থাপন করে।

• আলো ও আলোকবিজ্ঞান (Optics)

  আলোর প্রকৃতি, বৈশিষ্ট্য এবং এর মিথস্ক্রিয়া নিয়ে আলোচনা করে। লেন্স, আয়না, টেলিস্কোপ এবং অন্যান্য আলোকীয় যন্ত্র এর অন্তর্ভুক্ত।

• শব্দ ও তরঙ্গ (Sound and Waves)

  শব্দের উৎপত্তি, সঞ্চালন এবং বৈশিষ্ট্য, সেইসাথে অন্যান্য প্রকার তরঙ্গের (যেমন জলতরঙ্গ, বেতার তরঙ্গ) আলোচনা করে।

• বিদ্যুৎ ও চুম্বকত্ব (Electricity and Magnetism)

  আধান, তড়িৎ ক্ষেত্র, চৌম্বক ক্ষেত্র এবং তাদের মধ্যেকার সম্পর্ক নিয়ে আলোচনা করে। তড়িৎবর্তনী, জেনারেটর এবং মোটর এর গুরুত্বপূর্ণ অংশ।

• আধুনিক পদার্থবিজ্ঞান (Modern Physics)

  • আপেক্ষিকতা তত্ত্ব (Relativity)

    স্থান, সময় এবং আলোর গতির আপেক্ষিক প্রকৃতি নিয়ে আইনস্টাইনের তত্ত্ব আলোচনা করে।

  • কোয়ান্টাম বলবিদ্যা (Quantum Mechanics)

    পরমাণু এবং উপ-পারমাণবিক স্তরে পদার্থের আচরণ ব্যাখ্যা করে। এটি লেজার, ট্রানজিস্টর এবং অন্যান্য আধুনিক প্রযুক্তির ভিত্তি।

  • পারমাণবিক ও নিউক্লীয় পদার্থবিজ্ঞান (Atomic and Nuclear Physics)

    পরমাণুর গঠন, নিউক্লিয়াসের বৈশিষ্ট্য এবং তেজস্ক্রিয়তা নিয়ে আলোচনা করে।

  • কণা পদার্থবিজ্ঞান (Particle Physics)

    মৌলিক কণা এবং তাদের মিথস্ক্রিয়া নিয়ে গবেষণা করে।

  • কঠিন অবস্থা পদার্থবিজ্ঞান (Solid State Physics)

    কঠিন পদার্থের ভৌত বৈশিষ্ট্য নিয়ে আলোচনা করে, যা আধুনিক ইলেকট্রনিক্সের জন্য অত্যন্ত গুরুত্বপূর্ণ।

• জ্যোতির্পদার্থবিজ্ঞান ও মহাজাগতিক পদার্থবিজ্ঞান (Astrophysics and Cosmology)

  গ্রহ, নক্ষত্র, গ্যালাক্সি এবং মহাবিশ্বের উৎপত্তি ও বিবর্তন নিয়ে আলোচনা করে।

উপরে উল্লেখিত শাখাগুলি ছাড়াও পদার্থবিজ্ঞানের আরও অনেক বিশেষায়িত ক্ষেত্র রয়েছে। এই বিস্তৃত পরিসর থেকে বোঝা যায় যে পদার্থবিজ্ঞান আমাদের চারপাশের বিশ্বকে বোঝার জন্য একটি অপরিহার্য বিজ্ঞান।

পদার্থবিজ্ঞানের প্রয়োজনীয়তা

পদার্থবিজ্ঞান প্রকৃতির মৌলিক নিয়ম এবং নীতিগুলি বোঝার জন্য অপরিহার্য। এর প্রয়োজনীয়তা বহুমুখী এবং জীবনের বিভিন্ন ক্ষেত্রে বিস্তৃত। নিচে কয়েকটি গুরুত্বপূর্ণ দিক আলোচনা করা হলো:

প্রাকৃতিক জগৎ বোঝা

• মৌলিক নীতিগুলির জ্ঞান: পদার্থবিজ্ঞান আমাদের মহাবিশ্বের মৌলিক উপাদান, শক্তি, স্থান এবং সময়ের মতো ধারণাগুলি বুঝতে সাহায্য করে। এটি আলো, তাপ, শব্দ, বিদ্যুৎ, চৌম্বকত্ব এবং মহাকর্ষের মতো প্রাকৃতিক ঘটনাগুলির ব্যাখ্যা প্রদান করে।
• মহাবিশ্বের রহস্য উন্মোচন: জ্যোতির্বিদ্যা এবং কসমোলজির মাধ্যমে পদার্থবিজ্ঞান নক্ষত্র, গ্রহ, ছায়াপথ এবং মহাবিশ্বের উৎপত্তি ও বিবর্তন সম্পর্কে জ্ঞান দান করে।
• পৃথিবীর প্রক্রিয়া অনুধাবন: আবহাওয়া, জলবায়ু, ভূমিকম্প এবং আগ্নেয়গিরির মতো পৃথিবীর প্রাকৃতিক প্রক্রিয়াগুলি বুঝতে পদার্থবিজ্ঞানের নীতিগুলি অপরিহার্য।

প্রযুক্তিগত অগ্রগতি

• প্রকৌশল ও প্রযুক্তি: আধুনিক প্রযুক্তির প্রায় প্রতিটি ক্ষেত্র, যেমন ইলেকট্রনিক্স, কম্পিউটার, যোগাযোগ ব্যবস্থা, মহাকাশযান এবং চিকিৎসা সরঞ্জাম পদার্থবিজ্ঞানের জ্ঞান ছাড়া তৈরি করা সম্ভব নয়।
• নতুন উদ্ভাবন: পদার্থবিজ্ঞানের গবেষণা নতুন নতুন প্রযুক্তি এবং উপকরণের উদ্ভাবনের পথ খুলে দেয়, যা আমাদের জীবনযাত্রার মান উন্নত করে। উদাহরণস্বরূপ, লেজার, ফাইবার অপটিকস এবং সেমিকন্ডাক্টর প্রযুক্তির বিকাশ পদার্থবিজ্ঞানের অবদান।
• শক্তি উৎপাদন ও ব্যবহার: বিদ্যুৎ উৎপাদন (যেমন সৌর শক্তি, পারমাণবিক শক্তি), শক্তির সঞ্চয় এবং এর কার্যকর ব্যবহার পদার্থবিজ্ঞানের গুরুত্বপূর্ণ ক্ষেত্র।

অন্যান্য বিজ্ঞান ও জ্ঞানের শাখা

• রসায়ন: পদার্থের গঠন, বৈশিষ্ট্য এবং রাসায়নিক বিক্রিয়া বোঝার জন্য পদার্থবিজ্ঞানের নীতিগুলি ভিত্তি স্থাপন করে।
• জীববিজ্ঞান: জীবন্ত কোষের ভৌত প্রক্রিয়া, যেমন আলোসংশ্লেষণ, স্নায়ু সংকেত এবং জৈব অণুর গঠন বুঝতে পদার্থবিজ্ঞানের ধারণা গুরুত্বপূর্ণ।
• ভূ-বিজ্ঞান: পৃথিবীর গঠন, অভ্যন্তরীণ প্রক্রিয়া এবং প্রাকৃতিক সম্পদ অনুসন্ধানে পদার্থবিজ্ঞানের জ্ঞান প্রয়োজন।
• চিকিৎসা বিজ্ঞান: রোগ নির্ণয় (যেমন এক্স-রে, এমআরআই) এবং চিকিৎসায় (যেমন রেডিয়েশন থেরাপি) পদার্থবিজ্ঞানের নীতিগুলি ব্যবহৃত হয়।

সমস্যা সমাধান ও সমালোচনামূলক চিন্তাভাবনা

• বিশ্লেষণাত্মক দক্ষতা: পদার্থবিজ্ঞান অধ্যয়ন শিক্ষার্থীদের সমস্যা সমাধানের জন্য যৌক্তিক এবং বিশ্লেষণাত্মক চিন্তাভাবনার বিকাশ ঘটায়।
• গাণিতিক দক্ষতা: পদার্থবিজ্ঞানের সমস্যা সমাধানের জন্য গাণিতিক জ্ঞান এবং প্রয়োগের দক্ষতা বৃদ্ধি পায়।
• পরীক্ষণ ও পর্যবেক্ষণ: বৈজ্ঞানিক পদ্ধতির অংশ হিসেবে পরীক্ষণ এবং পর্যবেক্ষণের গুরুত্ব উপলব্ধি করতে সাহায্য করে।

পরিশেষে বলা যায়, পদার্থবিজ্ঞান কেবল একটি একাডেমিক বিষয় নয়, এটি আমাদের চারপাশের জগতকে বোঝার এবং উন্নত করার একটি অপরিহার্য হাতিয়ার। দৈনন্দিন জীবন থেকে শুরু করে অত্যাধুনিক প্রযুক্তি পর্যন্ত, প্রতিটি ক্ষেত্রে পদার্থবিজ্ঞানের অবদান অনস্বীকার্য।

ভৌত রাশি: মৌলিক ও লব্ধ

ভৌত জগতে যা কিছু পরিমাপ করা যায় তাকে রাশি বলে। এই ভৌত রাশিগুলোকে প্রধানত দুইটি ভাগে ভাগ করা যায়:

১. মৌলিক রাশি (Fundamental Quantities)

• যে সকল রাশি অন্য কোন রাশির উপর নির্ভর করে না অর্থাৎ স্বাধীন, তাদেরকে মৌলিক রাশি বলে।
• এই রাশিগুলো একে অপরের থেকে স্বতন্ত্র এবং এদেরকে অন্য কোন রাশির মাধ্যমে প্রকাশ করা যায় না।
• আন্তর্জাতিকভাবে স্বীকৃত মৌলিক রাশি ৭টি:
  • দৈর্ঘ্য (Length)
  • ভর (Mass)
  • সময় (Time)
  • তড়িৎ প্রবাহ (Electric Current)
  • তাপমাত্রা (Temperature)
  • দীপন তীব্রতা (Luminous Intensity)
  • পদার্থের পরিমাণ (Amount of Substance)

২. লব্ধ রাশি (Derived Quantities)

• যে সকল রাশি এক বা একাধিক মৌলিক রাশির সমন্বয়ে গঠিত হয় অথবা মৌলিক রাশির উপর নির্ভর করে, তাদেরকে লব্ধ রাশি বলে।
• এই রাশিগুলোকে মৌলিক রাশির মাধ্যমে প্রকাশ করা যায়।
• কয়েকটি উল্লেখযোগ্য লব্ধ রাশি:
  • ক্ষেত্রফল (Area) = দৈর্ঘ্য × প্রস্থ (দুটি মৌলিক রাশি দৈর্ঘ্যের গুণফল)
  • বেগ (Velocity) = দূরত্ব / সময় (মৌলিক রাশি দৈর্ঘ্য ও সময়ের ভাগফল)
  • ত্বরণ (Acceleration) = বেগ / সময় (মৌলিক রাশি দৈর্ঘ্য ও সময়ের সমন্বয়ে গঠিত বেগের সাথে সময়ের ভাগফল)
  • বল (Force) = ভর × ত্বরণ (মৌলিক রাশি ভর এবং লব্ধ রাশি ত্বরণের গুণফল)
  • কাজ (Work) = বল × সরণ (লব্ধ রাশি বল এবং মৌলিক রাশি দৈর্ঘ্যের গুণফল)
  • ক্ষমতা (Power) = কাজ / সময় (লব্ধ রাশি কাজ এবং মৌলিক রাশি সময়ের ভাগফল)
  • ঘনত্ব (Density) = ভর / আয়তন (মৌলিক রাশি ভর এবং লব্ধ রাশি আয়তনের ভাগফল)

পরিমাপ ও এর গুরুত্ব

পরিমাপ হলো কোনো কিছুর আকার, পরিমাণ, বা বৈশিষ্ট্য নির্ধারণ করার প্রক্রিয়া। এটি আমাদের চারপাশের জগৎকে বুঝতে এবং ব্যাখ্যা করতে অপরিহার্য। দৈনন্দিন জীবন থেকে শুরু করে বিজ্ঞান ও প্রযুক্তির প্রতিটি ক্ষেত্রে পরিমাপ গুরুত্বপূর্ণ ভূমিকা রাখে।

পরিমাপের গুরুত্ব:

• যোগাযোগ: সঠিক পরিমাপ তথ্যের আদান-প্রদানকে সহজ করে তোলে। যখন আমরা কোনো নির্দিষ্ট একক ব্যবহার করে কোনো কিছুর পরিমাণ উল্লেখ করি, তখন তা সকলের কাছে বোধগম্য হয়। উদাহরণস্বরূপ, "৫ মিটার লম্বা" বললে দৈর্ঘ্য সম্পর্কে একটি সুস্পষ্ট ধারণা পাওয়া যায়।
• তুলনা: পরিমাপের মাধ্যমে আমরা দুটি বা ততোধিক বস্তুর আকার, ওজন, বা অন্যান্য বৈশিষ্ট্য তুলনা করতে পারি। এর মাধ্যমে কোনটি বড়, কোনটি ছোট, বা কোনটির মান বেশি তা সহজেই নির্ণয় করা যায়।
• পরিকল্পনা ও নকশা: প্রকৌশল, স্থাপত্য, এবং অন্যান্য কারিগরি ক্ষেত্রে নির্ভুল পরিমাপ অপরিহার্য। কোনো কাঠামো নির্মাণ বা যন্ত্র তৈরি করার আগে সঠিক পরিমাপের মাধ্যমে নকশা প্রণয়ন করা হয়। সামান্য ভুল ত্রুটিও বড় ধরনের ক্ষতির কারণ হতে পারে।
• বৈজ্ঞানিক গবেষণা: বিজ্ঞান গবেষণার মূল ভিত্তি হলো পরিমাপ। বিভিন্ন পরীক্ষা-নিরীক্ষার মাধ্যমে প্রাপ্ত ডেটা পরিমাপের মাধ্যমেই সংগ্রহ ও বিশ্লেষণ করা হয়। এই পরিমাপের নির্ভুলতার উপর গবেষণার ফলাফল নির্ভরশীল।
• বাণিজ্য ও লেনদেন: ব্যবসা-বাণিজ্যে পণ্যের সঠিক ওজন, দৈর্ঘ্য, বা আয়তন নির্ধারণের জন্য পরিমাপ অত্যাবশ্যক। ক্রেতা এবং বিক্রেতা উভয়ের স্বার্থ রক্ষায় সঠিক পরিমাপ গুরুত্বপূর্ণ ভূমিকা পালন করে।
• গুণমান নিয়ন্ত্রণ: শিল্পকারখানায় উৎপাদিত পণ্যের গুণমান বজায় রাখার জন্য নিয়মিত পরিমাপ করা হয়। এর মাধ্যমে পণ্যের আকার, ওজন, বা অন্যান্য বৈশিষ্ট্য নির্দিষ্ট মান অনুযায়ী আছে কিনা তা নিশ্চিত করা হয়।
• নিরাপত্তা: অনেক ক্ষেত্রে পরিমাপ নিরাপত্তার জন্য গুরুত্বপূর্ণ। উদাহরণস্বরূপ, যানবাহনের গতিসীমা নির্ধারণ বা রাসায়নিক পদার্থের সঠিক অনুপাত বজায় রাখার জন্য পরিমাপ অপরিহার্য।

পরিশেষে বলা যায়, পরিমাপ আমাদের জীবনযাত্রার প্রতিটি স্তরে অত্যন্ত গুরুত্বপূর্ণ। সঠিক পরিমাপ কেবল তথ্য আদান-প্রদানই সহজ করে না, বরং পরিকল্পনা, গবেষণা, বাণিজ্য এবং নিরাপত্তাকেও নিশ্চিত করে। তাই পরিমাপের জ্ঞান অর্জন এবং এর সঠিক ব্যবহার অত্যন্ত জরুরি।

আন্তর্জাতিক একক পদ্ধতি (SI)

আন্তর্জাতিক একক পদ্ধতি (Systeme International d'Unites) হল মেট্রিক পদ্ধতির আধুনিক রূপ এবং এটি বিশ্বব্যাপী পরিমাপের সবচেয়ে বহুল ব্যবহৃত পদ্ধতি। এটি সাতটি মৌলিক এককের উপর ভিত্তি করে গঠিত:

• দৈর্ঘ্য: মিটার (m)
• ভর: কিলোগ্রাম (kg)
• সময়: সেকেন্ড (s)
• তড়িৎ প্রবাহ: অ্যাম্পিয়ার (A)
• তাপমাত্রা: কেলভিন (K)
• আলোর তীব্রতা: ক্যান্ডেলা (cd)
• পদার্থের পরিমাণ: মোল (mol)

এই মৌলিক এককগুলো ব্যবহার করে অন্যান্য ভৌত রাশির জন্য লব্ধ একক তৈরি করা হয়। এসআই পদ্ধতি বিজ্ঞান, প্রকৌশল, বাণিজ্য এবং দৈনন্দিন জীবনে পরিমাপের ক্ষেত্রে একটি সুসংগত এবং সার্বজনীন কাঠামো প্রদান করে। এর স্পষ্ট সংজ্ঞা এবং সহজ ব্যবহারযোগ্যতার কারণে এটি বিশ্বব্যাপী ব্যাপকভাবে গৃহীত হয়েছে।

রাশির মাত্রা ও এককের উপসর্গ

রাশির মাত্রা (Dimensions of Physical Quantities)

ভৌত রাশিসমূহের মাত্রা হলো ঐ সকল সূচক যা ঐ রাশির একক গঠনে মৌলিক রাশিগুলোর (যেমন - দৈর্ঘ্য [L], ভর [M], সময় [T], তড়িৎ প্রবাহ [I], তাপমাত্রা [Θ], আলোর তীব্রতা [J], পদার্থের পরিমাণ [N]) উপর আরোপ করা হয়।

উদাহরণস্বরূপ:

• বেগের মাত্রা: \([LT^{-1}]\) (দৈর্ঘ্য/সময়)
• ত্বরণের মাত্রা: \([LT^{-2}]\) (দৈর্ঘ্য/সময়²)
• বলের মাত্রা: \([MLT^{-2}]\) (ভর × দৈর্ঘ্য/সময়²)
• কাজের মাত্রা: \([ML^2T^{-2}]\) (বল × দৈর্ঘ্য)

এককের উপসর্গ (Prefixes of Units)

এককের উপসর্গ হলো সেই সকল প্রতীক যা এসআই (আন্তর্জাতিক একক পদ্ধতি) এককের পূর্বে গুণিতক হিসেবে ব্যবহৃত হয়। এগুলো খুব ছোট বা খুব বড় মানকে সহজে প্রকাশ করতে সাহায্য করে।

কয়েকটি গুরুত্বপূর্ণ উপসর্গ এবং তাদের মান:

উপসর্গ	প্রতীক	গুণিতক
টেট্রা	T	\(10^{12}\)
গিগা	G	\(10^9\)
মেগা	M	\(10^6\)
কিলো	k	\(10^3\)
হেক্টো	h	\(10^2\)
ডেকা	da	\(10^1\)
ডেসি	d	\(10^{-1}\)
সেন্টি	c	\(10^{-2}\)
মিলি	m	\(10^{-3}\)
মাইক্রো	µ	\(10^{-6}\)
ন্যানো	n	\(10^{-9}\)
পিকো	p	\(10^{-12}\)

উদাহরণস্বরূপ:

• 1 কিলোমিটার (km) = \(10^3\) মিটার
• 1 মিলিমিটার (mm) = \(10^{-3}\) মিটার
• 1 মেগাওয়াট (MW) = \(10^6\) ওয়াট
• 1 মাইক্রোসেকেন্ড (µs) = \(10^{-6}\) সেকেন্ড

পরিমাপের নির্ভুলতা ও যথার্থতা

পরিমাপের ক্ষেত্রে নির্ভুলতা (Accuracy) এবং যথার্থতা (Precision) দুটি গুরুত্বপূর্ণ ধারণা। এই দুটি ধারণা প্রায়শই একে অপরের সাথে গুলিয়ে ফেলা হয়, তবে এদের মধ্যে সুস্পষ্ট পার্থক্য রয়েছে।

নির্ভুলতা (Accuracy)

নির্ভুলতা বলতে বোঝায় একটি পরিমাপকৃত মান কতখানি সত্য মানের (True Value) কাছাকাছি। যদি কোনো পরিমাপের গড় মান সত্য মানের খুব কাছে হয়, তবে সেই পরিমাপকে নির্ভুল বলা হয়। নির্ভুলতা ত্রুটির (Error) উপর নির্ভর করে। ত্রুটি যত কম, নির্ভুলতা তত বেশি।

উদাহরণ: মনে করুন একটি বস্তুর প্রকৃত দৈর্ঘ্য ১০ সেন্টিমিটার। যদি কোনো পরিমাপক যন্ত্রের সাহায্যে কয়েকবার পরিমাপ করে মানগুলো পাওয়া যায়: ৯.৯ সেমি, ১০.১ সেমি, ১০.০ সেমি, ৯.৮ সেমি, ১০.২ সেমি। এই মানগুলোর গড় (৯.৯ + ১০.১ + ১০.০ + ৯.৮ + ১০.২) / ৫ = ১০.০ সেমি। যেহেতু গড় মান প্রকৃত মানের খুব কাছাকাছি, তাই এই পরিমাপগুলো নির্ভুল বলা যেতে পারে।

যথার্থতা (Precision)

যথার্থতা বলতে বোঝায় একটি পরিমাপ কতখানি সূক্ষ্মভাবে করা হয়েছে অথবা একই পদ্ধতিতে বারবার পরিমাপ করলে প্রাপ্ত মানগুলো একে অপরের কতটা কাছাকাছি থাকে। যথার্থতা পুনরাবৃত্তিযোগ্যতার (Repeatability) উপর নির্ভর করে। যদি একাধিকবার পরিমাপ করে প্রায় একই মান পাওয়া যায়, তবে সেই পরিমাপকে যথার্থ বলা হয়।

উদাহরণ: অন্য একটি পরিমাপক যন্ত্রের সাহায্যে যদি একই বস্তুর দৈর্ঘ্য কয়েকবার পরিমাপ করে মানগুলো পাওয়া যায়: ১০.০২ সেমি, ১০.০৩ সেমি, ১০.০১ সেমি, ১০.০২ সেমি, ১০.০২ সেমি। এই মানগুলো একে অপরের খুব কাছাকাছি, তাই এই পরিমাপগুলো যথার্থ বলা যেতে পারে। তবে এই পরিমাপগুলোর গড় (১০.০২ + ১০.০৩ + ১০.০১ + ১০.০২ + ১০.০২) / ৫ = ১০.০২ সেমি, যা প্রকৃত মান (১০ সেমি) থেকে সামান্য দূরে। সুতরাং, এই পরিমাপগুলো যথার্থ হলেও নির্ভুল নাও হতে পারে।

নির্ভুলতা ও যথার্থতার মধ্যে সম্পর্ক

একটি পরিমাপ নির্ভুল হতে পারে কিন্তু যথার্থ নাও হতে পারে, আবার যথার্থ হতে পারে কিন্তু নির্ভুল নাও হতে পারে। সর্বোত্তম পরিমাপ হল সেটি যা একই সাথে নির্ভুল এবং যথার্থ।

তুলনা করার জন্য একটি উদাহরণ:

• উচ্চ নির্ভুলতা, নিম্ন যথার্থতা: ৯.৮ সেমি, ১০.৩ সেমি, ৯.৯ সেমি, ১০.২ সেমি (গড় = ১০.০ সেমি, মানগুলো একে অপরের থেকে দূরে)
• নিম্ন নির্ভুলতা, উচ্চ যথার্থতা: ১১.২ সেমি, ১১.৩ সেমি, ১১.২ সেমি, ১১.৩ সেমি (গড় = ১১.২ সেমি, মানগুলো একে অপরের কাছে)
• উচ্চ নির্ভুলতা, উচ্চ যথার্থতা: ১০.০ সেমি, ১০.১ সেমি, ৯.৯ সেমি, ১০.০ সেমি (গড় = ১০.০ সেমি, মানগুলো একে অপরের কাছে)
• নিম্ন নির্ভুলতা, নিম্ন যথার্থতা: ৯.৫ সেমি, ১০.৫ সেমি, ৯.৬ সেমি, ১০.৪ সেমি (গড় = ১০.০ সেমি, মানগুলো একে অপরের থেকে দূরে)

পরিমাপের গুণমান নিশ্চিত করার জন্য নির্ভুলতা এবং যথার্থতা উভয়ই গুরুত্বপূর্ণ।

সরল যন্ত্রপাতি দ্বারা পরিমাপ (মিটার স্কেল, ভার্নিয়ার স্কেল, স্লাইড ক্যালিপার্স, স্ক্রু-গেজ, থামা ঘড়ি, ব্যালেন্স)

১. মিটার স্কেল

মিটার স্কেল হলো দৈর্ঘ্য পরিমাপের একটি সরল যন্ত্র। এটি সাধারণত ১ মিটার দৈর্ঘ্যের এবং সেন্টিমিটারে দাগাঙ্কিত থাকে। এর সাহায্যে কোনো বস্তুর দৈর্ঘ্য সরাসরি মিলিমিটার পর্যন্ত নির্ভুলভাবে মাপা যায়।

• ব্যবহার: কোনো সরলরেখার দৈর্ঘ্য, কোনো বস্তুর দৈর্ঘ্য ও প্রস্থ ইত্যাদি পরিমাপ করতে এটি ব্যবহৃত হয়।
• নূন্যতম গণনা: সাধারণত ১ মিলিমিটার।

২. ভার্নিয়ার স্কেল

ভার্নিয়ার স্কেল মূল স্কেলের সাথে যুক্ত একটি ছোট অতিরিক্ত স্কেল। এটি মূল স্কেলের ক্ষুদ্রতম ভাগের ভগ্নাংশের নির্ভুল পরিমাপ নিতে সাহায্য করে। ভার্নিয়ার ক্যালিপার্সে এটি প্রধানত ব্যবহৃত হয়।

• ব্যবহার: কোনো চোঙের ভেতরের ও বাইরের ব্যাস, কোনো বস্তুর গভীরতা ইত্যাদি সূক্ষ্মভাবে পরিমাপ করতে এটি ব্যবহৃত হয়।
• নূন্যতম গণনা: ভার্নিয়ার ধ্রুবকের উপর নির্ভরশীল (সাধারণত ০.১ মিলিমিটার বা ০.০২ মিলিমিটার)।

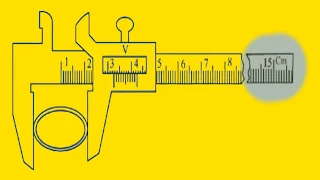
৩. স্লাইড ক্যালিপার্স

স্লাইড ক্যালিপার্স একটি বহুল ব্যবহৃত দৈর্ঘ্য পরিমাপক যন্ত্র। এতে একটি মূল স্কেল এবং একটি স্লাইডিং ভার্নিয়ার স্কেল থাকে। এর সাহায্যে ভেতরের ব্যাস, বাইরের ব্যাস এবং গভীরতা পরিমাপ করা যায়।

• ব্যবহার: ছোট আকারের বস্তুর দৈর্ঘ্য, প্রস্থ, উচ্চতা, ভেতরের ও বাইরের ব্যাস এবং গভীরতা পরিমাপের জন্য এটি খুবই উপযোগী।
• নূন্যতম গণনা: ভার্নিয়ার ধ্রুবকের উপর নির্ভরশীল (সাধারণত ০.১ মিলিমিটার বা ০.০২ মিলিমিটার)।

৪. স্ক্রু-গেজ

স্ক্রু-গেজ একটি সূক্ষ্ম দৈর্ঘ্য পরিমাপক যন্ত্র। এটি স্ক্রু এবং পিচ নীতির উপর ভিত্তি করে কাজ করে। এর সাহায্যে খুব ছোট দৈর্ঘ্যের (যেমন তারের ব্যাস, পাতলা পাতের পুরুত্ব) অত্যন্ত নির্ভুল পরিমাপ নেওয়া যায়।

• ব্যবহার: সরু তারের ব্যাস, ধাতব পাতের পুরুত্ব, ছোট গোলকের ব্যাস ইত্যাদি অত্যন্ত সূক্ষ্মভাবে পরিমাপ করতে এটি ব্যবহৃত হয়।
• নূন্যতম গণনা: স্ক্রু-গেজের পিচ এবং বৃত্তাকার স্কেলের ভাগের সংখ্যার উপর নির্ভরশীল (সাধারণত ০.০১ মিলিমিটার বা ০.০০১ মিলিমিটার)।

৫. থামা ঘড়ি (স্টপওয়াচ)

থামা ঘড়ি হলো সময় পরিমাপের একটি সরল যন্ত্র। এর সাহায্যে কোনো নির্দিষ্ট ঘটনার শুরু থেকে শেষ পর্যন্ত অতিবাহিত সময় নির্ণয় করা যায়। অ্যানালগ ও ডিজিটাল দুই ধরনের থাম ঘড়ি পাওয়া যায়।

• ব্যবহার: খেলাধুলা, বৈজ্ঞানিক পরীক্ষা-নিরীক্ষা এবং অন্যান্য সময়-নির্ভর ঘটনার সময়কাল মাপার জন্য এটি ব্যবহৃত হয়।
• নূন্যতম গণনা: সাধারণত ০.১ সেকেন্ড বা ০.০১ সেকেন্ড পর্যন্ত হতে পারে।

৬. ব্যালেন্স (নিত্য পাল্লা বা সাধারণ তুলাযন্ত্র)

ব্যালেন্স বা তুলাযন্ত্র হলো কোনো বস্তুর ভর পরিমাপের একটি সরল যন্ত্র। এটি মূলত একটি লিভার যা একটি নির্দিষ্ট বিন্দুতে (ফালক্রাম) স্থাপিত থাকে এবং এর দুই প্রান্তে দুটি পাল্লা থাকে। অজানা ভরের বস্তুকে এক পাল্লায় রেখে অন্য পাল্লায় পরিচিত ভরের বাটখারা চাপিয়ে ভারসাম্য আনা হয়।

• ব্যবহার: কোনো বস্তুর ভর নির্ণয়ের জন্য এটি ব্যবহৃত হয়। রসায়ন, পদার্থবিজ্ঞান এবং দৈনন্দিন জীবনে বিভিন্ন জিনিসপত্রের ভর মাপার জন্য এটি অপরিহার্য।
• নূন্যতম গণনা: ব্যবহৃত বাটখারার ক্ষুদ্রতম ভরের উপর নির্ভরশীল (বিভিন্ন ধরনের ব্যালেন্সের জন্য বিভিন্ন)।

উপসংহার

ভৌত রাশি ও পরিমাপ পদার্থবিজ্ঞানের ভিত্তি রচনা করে। এ অধ্যায় আমাদের শেখায় কিভাবে কোনো ঘটনাকে পরিমাপযোগ্য রূপে উপস্থাপন করতে হয় এবং তার যথাযথ বিশ্লেষণ করতে হয়। এই জ্ঞান ভবিষ্যতের অধ্যায়গুলোর জন্য একটি মজবুত ভিত্তি গড়ে তোলে এবং আমাদেরকে বিজ্ঞানের প্রকৃত চেতনার সাথে পরিচিত করে।